Бифуркация

Оглавление

Притча об осле

Проиллюстрировать сложные понятия легче всего на простых и жизненных примерах. Кто не помнит притчу про буриданова осла, напомним.

Иначе еще говорят, что это момент своевременной просьбы.

Прием нужного момента широко используется в детской педагогике и в психологии семейных отношений. Да и в любой сфере это правило работает, и о нем нужно помнить.

Пример из психологии животных. Когда котенок приучится писать в горшок, вы будете наказывать его через час после пакости или когда поймаете на месте преступления? Механизм прост и ясен – в отношении людей все то же, только без насилия.

Что такое бифуркация простыми словами

Термин бифуркация произошел от латинского bifurcus(«раздвоенный»). В основе значения понятия лежат множественные преобразования или метаморфозы все возможных объектов по средству происходящего процесса изменения значимых параметров.

Для общего понимания понятия рассмотрим следующие примеры бифуркации:

В биологии это симметричное деление бронхиального дерева, либо преобразование одного сосуда в два, равных по диаметру.
В географии это расхождение русла реки на два разнонаправленных рукава.
В научной фантастике в качестве примера можно привести параллельные разновременные отрезки, отвечающие за важные события, происходящие с персонажем.
В образовании бифуркация понимается как разные учебно-методические направления одного класса.
В жизни среднестатистического человека выступает в качестве кризисного момента, после которого полностью меняется образ жизни индивида.

Как проводится диагностика

Диагностика патологического процесса в области бифукрации корней зуба включает в себя несколько исследований. Обязательно проводится рентгенологическое обследование – более информативна здесь именно компьютерная томография, которая показывает мельчайшие изменения. Также стоматолог проводит зондирование десневого кармана (в норме десна не должна отходить от зуба более чем на 3 мм).

Важно знать! При необходимости снимается искусственная коронка или убирается старая пломба и зубная полость изучается на наличие перфораций. Оптимально, если при таком обследовании врач пользуется микроскопом – ведь при многократном увеличении можно разглядеть мельчайшие дефекты

Если патология в области бифуркации возникла в ходе лечения, то стоматолог должен обратить внимание на появление крови в полости. В этом случае можно с 99% уверенностью говорить именно о перфорации, которая нуждается в скорейшей реставрации

3.1 Понятие мягкой и жесткой потери устойчивости

Бифуркации условно можно разделить на мягкие и жёсткие, что наглядно демонстрируется следующим примером. На рис. 3.1 и рис. 3.2 изображён перестраиваемый профиль с шариком. В результате изменения какого-либо фактора (параметра), исходный профиль изменяет свою конфигурацию таким образом, что устойчивое равновесное состояние шарика теряется. При этом «рождаются» два новых устойчивых состояния равновесия, в один из которых и сваливается шарик. Вновь появившиеся состояния равновесия перестроившегося профиля располагаются в непосредственной близости от начального состояния равновесия, которое потеряло устойчивость. Бифуркации такого типа называют мягкими. Новый режим функционирования как бы постепенно появляется из режима, потерявшего устойчивость, и сосуществует рядом с ним.

Рис. 3.1 — перестраиваемый профиль с шариком

Характер перестроения профиля, изображённого на рис. 3.2, иной. Для значения параметра меньше критического шарик находится в устойчивом равновесном состоянии. Одновременно существует ещё одно потенциальное неустойчивое равновесное состояние. При перестроении профиля для критического значения параметра устойчивое и неустойчивое состояния сливаются в одно. Далее они оба исчезают, и система «скачком» выбирает новый режим, который существенно отличается от предыдущего и не находится в непосредственной близости от исходного режима. Бифуркации такого типа относятся к жёстким. Именно жёсткие (скачкообразные) бифуркации в первую очередь являются предметом исследования теории катастроф.

Рис. 3.2 — перестраиваемый профиль с шариком

4. Виды бифуркаций

В следующем разделе будут описаны основные виды и примеры бифуркаций как непрерывных, так и дискретных (отражений) функций.

Конкретные примеры в биологии

Сети с бифуркацией в своей динамике контролируют многие важные переходы в клеточном цикле . Все переходы , и действуют как биохимические переключатели в клеточном цикле . Например, яичные экстракты Xenopus laevis необратимо втягиваются в митоз и выходят из него за счет положительной обратной связи при фосфорилировании Cdc2, циклин-зависимой киназы .

В популяционной экологии динамика сетей взаимодействий пищевой сети может демонстрировать бифуркации Хопфа . Например, в водной системе, состоящей из первичного продуцента , минерального ресурса и травоядного животного, исследователи обнаружили, что закономерности равновесия, цикличности и исчезновения популяций можно качественно описать с помощью простой нелинейной модели с бифуркацией Хопфа.

Утилизацию галактозы у почкующихся дрожжей (S. cerevisiae) можно измерить по экспрессии GFP, индуцированной промотором GAL, в зависимости от изменения концентрации галактозы. В системе наблюдается бистабильное переключение между индуцированным и неиндуцированным состояниями.

Точно так же утилизация лактозы в E. coli как функция концентрации тиометилгалактозида (аналог лактозы), измеренная с помощью GFP-экспрессирующего промотора lac, демонстрирует бистабильность и гистерезис (рис. 10, слева и справа, соответственно).

2.1 Бифуркации в системах с простым движением

Негрубость системы означает негрубость тех или иных траекторий. Среди таких траекторий прежде всего выделяются устойчивые состояния равновесия и периодические движения, поскольку они являются математическим образом стационарных состояний и автоколебаний.

Состояние равновесия n-мерной системы \(\mathop x\limits^. = X(x)\) точка \(M({x^*})\), где \({x^*}\) — решение системы \(X(x) = 0\). Оно негрубое, если среди \({\lambda _{1,}}{\lambda _2}, …{\lambda _n}\) — корней характеристического уравнения \(\det (\frac{{\partial X({x^*})}}{{\partial x}} — \lambda E) = 0\) имеются корни, лежащие на мнимой оси. В случае, если \({\mathop{\rm Re}\nolimits} {\lambda _i} < 0,i = 1,…n \), состояние равновесия является устойчивым. Если имеются корни как с отрицательной, так и с положительной реальной частью, то состояние равновесия носит название седлового. К нему будут стремиться траектории как при \(t \to + \infty \), так и при \(t \to — \infty \) , в совокупности образуя устойчивое \({W^s}\) и неустойчивое \({W^u}\) многообразия. Периодическое решение \(x = \phi (t) \) этой системы будет негрубым, если среди мультипликаторов \({\rho _1},{\rho _2},…{\rho _{n — 1}}\) имеются равные по модулю 1. Если же \(\left| {{\rho _i}} \right| < 1\), периодическое движение устойчивое, и седловое, если среди мультипликаторов есть как лежащие внутри единичного круга, так и вне его.

В настоящее время основные (коразмерности 1) локальные и глобальные бифуркации таких траекторий подробно изучены.

Устойчивое состояние равновесия может:

исчезнуть, слившись с неустойчивым. В момент бифуркации у состояния равновесия, называемого седло-узел, только один характеристический корень лежит на мнимой оси и равен нулю.
потерять устойчивость. При этом из состояния равновесия будет рождаться (влипать в него) устойчивое (неустойчивое) периодическое движение, если в момент бифуркации состояние равновесия устойчиво (неустойчиво). Эта бифуркация, объясняющая генерацию колебаний, носит название Андронова-Хопфа.

Устойчивое периодическое движение может:

исчезнуть, слившись с неустойчивым в момент бифуркации. Для \(n > 2\) негрубое периодическое движение носит название седло-узлового.
потерять устойчивость с рождением устойчивого
- периодического движения удвоенного периода, если мультипликатор равен (-1),
- двумерного инвариантного тора, если \({\rho _{1,2}} = {e^{ \pm i\phi }}\), где \(\phi \ne 0,\pi ,\frac{\pi }{2},\frac{{2\pi }}{3}\).

Устойчивые периодические движения могут также рождаться в результате следующих глобальных бифуркаций:

из траектории, идущей из седла с характеристическими корнями \({\mathop{\rm Re}\nolimits} {\lambda _i} < 0\), \(i=1, … ,n-1\), и седловой величиной \( \max {\mathop{\rm Re}\nolimits} {\lambda _i} + {\lambda _n} < 0\) в то же седло,
из траектории, идущей из седло-узла в него при исчезновении состояния равновесия,
при исчезновении седло-узлового периодического движения, все траектории неустойчивого многообразия которого, образуют в совокупности сильно сжимающуюся трубку, навивающуюся на периодическое движение. Эта бифуркация называется «катастрофой голубого неба» и ее особенность состоит в том, что при стремлении параметра к бифуркационному значению длина периодических движений стремится к бесконечности.

В случае коразмерности 1 седловые периодические движения могут рождаться из траектории, идущей 1) из седла в него же, 2) из негрубого состояния равновесия типа седло-седло в него же при его исчезновении (такое состояние равновесия образуется при слиянии двух грубых седел.)

Все перечисленные бифуркации не выводят из класса систем с простым поведением траекторий.

Разделение аорты

Аорта делится на артерии (общие подвздошные) в области четвертого поясничного позвонка. Эти сосуды длиной около 6 см направлены вниз и вбок под углом 30-60°. Левая общая подвздошная артерия чуть короче правой. Правая в районе соединения подвздошной кости с боковым отделом крестца делится на наружный и внутренний сосуд – по ним снабжаются кровью органы брюшины и ноги.

Точка бифуркации – слабое место аорты, здесь сосуд часто подвергается расслоению из-за постоянно повышенного кровяного давления. Кровь, разделяясь, завихряется и негативно воздействует на стенку аорты в месте бифуркации, провоцируя развитие:

аневризмы – возникает из-за утраты сосудами эластичности и прочности. Пациенты нуждаются в срочной терапии – велика вероятность расслоения аневризмы, разрыва аорты и более серьезных последствий;
тромбоза (синдром Лериша) – чаще диагностируется у пациентов преклонного возраста с атеросклерозом. Развивается медленно, при адекватном лечении прогноз благоприятный;
эмболии – способна вызвать непроходимость крови, ишемические поражения сосудов ног, органов брюшины и таза. Требует хирургического вмешательства.

При развитии патологий бифуркации аорты нередко страдают почечные и общие подвздошные артерии. У четверти больных поражение распространяется еще дальше. Состоянию характерны выраженные боли. При перемежающейся хромоте, обусловленной поражением бифуркации аорты, они локализуются в бедрах и мышцах ягодиц. У мужчин патология понижает половое влечение и вызывает ослабление эрекции, иногда даже импотенцию.

https://youtube.com/watch?v=vDlZxnrNxUE

https://youtube.com/watch?v=Hs-WPp3IT38

https://youtube.com/watch?v=JbSHUFsoLK8

Заметки

Blanchard, P .; Девани, Р.Л.; Холл, Г. Р. (2006). Дифференциальные уравнения. Лондон: Томпсон. С. 96–111. ISBN 978-0-495-01265-8.
Анри Пуанкаре. «L’Équilibre d’une masse fluide animée d’un mouvement de Rotation«. Acta Mathematica, vol.7, pp. 259-380, сентябрь 1885 г.
Строгац, Стивен Х. (1994). Нелинейная динамика и хаос. Эддисон-Уэсли. п. 262. ISBN 0-201-54344-3.
Ло, Динцзюнь (1997). Теория бифуркаций и методы динамических систем.. World Scientific. п. 26. ISBN 981-02-2094-4.
Джеймс П. Кинер, «Бифуркация бесконечного периода и ветви глобальной бифуркации», Журнал SIAM по прикладной математике, Vol. 41, № 1 (август 1981 г.), стр. 127–144.
Гуцвиллер, Мартин К. (1990). Хаос в классической и квантовой механике. Нью-Йорк: Springer-Verlag. ISBN 978-0-387-97173-5.

Ипостаси понятия

Под бифуркацией обычно понимают состояние системы, поставленной перед выбором варианта развития (развилка дорог). Понятие используют в разных отраслях:

медицина – деление трахеи и крупных сосудов на две ветки, расходящиеся под равными углами;
география – разветвление речного русла;
механика – обретение системой новых свойств при смене ее параметров;
литература – разделение времени и пространства на два потока с разными событиями (параллельные реальности);
математика – ветвление решений нелинейного дифференциального уравнения;
философия – закономерность двойственности («Ян-Инь», мужское-женское).

В точке бифуркации (на развилке дорог) система не имеет достаточного равновесия. Самые незначительные случайности могут абсолютно изменить вектор дальнейшей эволюции, лишая систему шанса развиваться альтернативным путем. В жизни человека бифуркация – точка перелома, кардинально меняющая его жизнь.

https://youtube.com/watch?v=yX3hyLBBW44

https://youtube.com/watch?v=UPKTX2s-AlI

https://youtube.com/watch?v=iV3nThwaTq4

Диагностика и терапия патологии

Для выявления негативных изменений бифуркации сосуда нужно пройти медицинское обследование:

ангиографию – контрастное рентгенологическое исследование сосудов;
флоуметрию (ультразвуковую и электромагнитную) – количественное определение кровотока в крупных сосудах;
сегментарную объемную сфигмографию – измерение пульсовых колебаний сосудистых стенок;
продольную сегментарную реографию – оценка регионарной гемодинамики.

Терапию проводят после диагностики, определения причин возникновения патологии, изучения симптоматики и выявления сочетанных заболеваний. Лечение может быть медикаментозным и хирургическим, это зависит от тяжести протекания болезни, общего состояния больного и его возраста. Иногда в бифуркационные стенозы устанавливают «предназначенные» стенты (устройство, обеспечивающее расширение участка артерии). Это асимметричные стенты, отличные от линейных. Они рассчитаны на имплантацию в места удвоения сосуда.

Наиболее эффективным способом оперативного вмешательства на бифуркацию сонной артерии считают эндартерэктомию с пластикой внутренней сонной артерии заплатой и установкой стента. При выборе заплаты учитывают механические свойства ее материала. Стент существенно влияет на состояние сосудистой стенки и улучшает гемодинамику.

Наибольшее распространение термин «бифуркация» получил именно в медицине. Разделение трахеи и сосудов на две примерно равнозначные ветви имеет большое функциональное значение. К примеру, бифуркация аорты обеспечивает стабильное снабжение кровью обеих нижних конечностей. Но место раздвоения сосудов весьма уязвимо для негативных воздействий, что всегда учитывается специалистами при проведении диагностических мероприятий.

Точка бифуркации в истории

В государственно-политическом устройстве точку бифуркации иллюстрирует выбор религии для Киевской Руси князем Владимиром. Когда стоял выбор между православием, исламом и иудаизмом, близость к культуре Византии стала тем параметром, который определил путь развития государства.

В истории роль случайных флуктуаций, приводящих к точке бифуркации, чрезвычайно велика. Сколько побед великих полководцев произошли не благодаря их умениям и стратегии, а только в результате цепи совершенно случайных событий!

Так, перед нашествием монголо-татар Русь имела неустойчивую государственную структуру, и развитие могло пойти по разным сценариям. Но нашествие монголов повернуло ее в сторону деспотизма с восточным уклоном. Симбиоз восточного деспотизма, византийско–имперских идей и тевтонского территориального управления на долгие века установили режим поверхностного права, использования административного ресурса и попрания всех прав человека.

Точки бифуркации в кинематографе и литературе

Идея бифуркации времени – пространства давно и прочно закрепилась в литературе и кинематографе. Начиная со старика Хоттабыча и заканчивая голливудским бестселлером «Назад в будущее», тема параллельности времени и пространства занимает умы творческой интеллигенции. Наиболее полно и структурированно к изложению этой темы подходит современный американский прозаик Ричард Бах в романе «Единственная».

Мы все приходим к пониманию, что каждую секунду нашей жизни в момент выбора мы находимся в точке бифуркации. И маятник нашей жизни качнется – вопрос лишь в том, насколько наш сознательный выбор повлияет на направление его движения. Понимание равновесности и прихода в состояние нестабильности системы — не теоретические изыскания ученых мужей. Это прикладная часть знаний, обладание которой поможет каждому сделать правильный выбор.

Почему возникают проблемы

Вовлечение области фуркации в патологический процесс возникает в двух случаях:

извне (через десну или кость) проникает инфекция: в норме область фуркации плотно соприкасается с периодонтом и костными стенками зубной лунки. Но если кость начала проседать (что происходит при пародонтите, пародонтозе), то область фуркации становится доступной для микробов из внешней среды. Также воспаление кости (например, когда инфекция попала в нее с током крови) приводит к «расплавлению» зубных тканей. Со временем цемент корня разрушается, в зубе появляется отверстие, а в пульпу проникают микробы,
изнутри зуба: например, при пульпите или перфорации дна пульпарной камеры (во время сверления или прохождения корневых каналов), которая как раз расположена над областью фуркации. В этом случае микробы из полости рта проникают в костную лунку, вызывая ее воспаление.

4.4 Бифуркация Андронова – Хопфа (Hopf)

Кроме бифуркаций состояний равновесия в динамических системах при изменении параметра может происходить ещё одна перестройка структуры фазового портрета. Этот тип бифуркации рассматривает рождение предельного цикла из неподвижной точки и является более сложным, чем представленные выше.
Пусть нелинейная модель описывается следующим д. у.:

где \(z \) – комплексная переменная; \(\mu + j\eta \) – комплексный параметр, причём \(j \) – мнимая единица, \(\mu \) – варьируемый бифуркационный параметр.

Уравнение представляет собой комплексный аналог бифуркации типа «вилка». С целью определения всех равновесных решений необходимо произвести замену комплексной переменной \(z \):

где \({x_1}\) и \({x_2}\) новые вещественные переменные.

В результате подстановки \(z \) в исходное ДУ получается система из двух уравнений первого порядка:

\{x_1} — \eta {x_2}\\
{{\dot x}_2} = {x_2} + \eta {x_1}
\end{array}\]

Таким образом, здесь осуществлён переход к модели второго порядка с вещественными параметрами. Полученные уравнения связаны между собой через комплексную переменную \(z \) и имеют следующие два стационарных решения:

Первое решение является неустойчивым и совпадает с точкой бифуркации, а второе решение определяет окружность радиуса \(\sqrt \mu\) в пространстве координат \(({x_1},\;{x_2},\;\mu )\). На рис. 4.5 изображены фазовые траектории при фиксированных \(\mu \).

Рис. 4.5 — Фазовый портрет системы с бифуркацией Андронова – Хопфа

Теория бифуркации

Данная теория универсальна, она применима ко всем системам (математическим, физическим и т.д.), где отмечены фазовые изменения последовательности, скачки реальной системы.

Можно выделить три основных типа фундаментальных изменений точки бифуркации:

Перелом, изменение траектории движения.
Выбор, т.е. смена параметра.
Упорядоченность, по средству скачка происходит переход в новое состояние устойчивости.

Знание порядка изменения облегчает исследовательские мероприятия, помогает предугадать характер новых движений, при переходе в качественно другое состояние, основной системы и многое другое.

Современные методы лечения

При обнаружении патологии в области бифуркации корней возникает закономерный вопрос – стоит ли сохранять зуб? Точно ответить может только стоматолог после тщательной диагностики, т.к. здесь существует множество определяющих факторов

Важно правильно сделать прогноз «работоспособности» зуба, если будет выбрано именно лечение – чтобы не началось сильное воспаление десен и кости (которое, кстати, может затронуть корни соседних зубов)

Терапевтическое лечение

Консервативное лечение области бифуркации возможно, если размер отверстия не превышает 1 мм, и чаще всего осуществляется по следующим технологиям:

закрытие перфорации специальными пломбировочными материалами: это могут быть стеклоиономерные цементы, поглощающие влагу – поскольку качественно высушить рабочую зону не представляется возможным. Здесь подойдут марки для пломбирования корневых каналов ProRoot MTA, MTA-Angelus,
закрытие перфорации при помощи препаратов кальция: они восстанавливают структуру поврежденных тканей (которые в основном и состоят из кальция),
армирование металлическими нитями и пломбирование отверстия в области бифуркации.

Во всех вышеперечисленных случаях после реставрации отверстия в области бифуркации полость зуба закрывается временной пломбой, а пациент через 5-7 дней приходит на контрольный рентген, чтобы оценить качество закрытия перфорации. Таких визитов может быть несколько. После достижения положительного результата (перфорация полностью закрыта, возле корней отсутствует воспаление) устанавливается постоянная пломба.

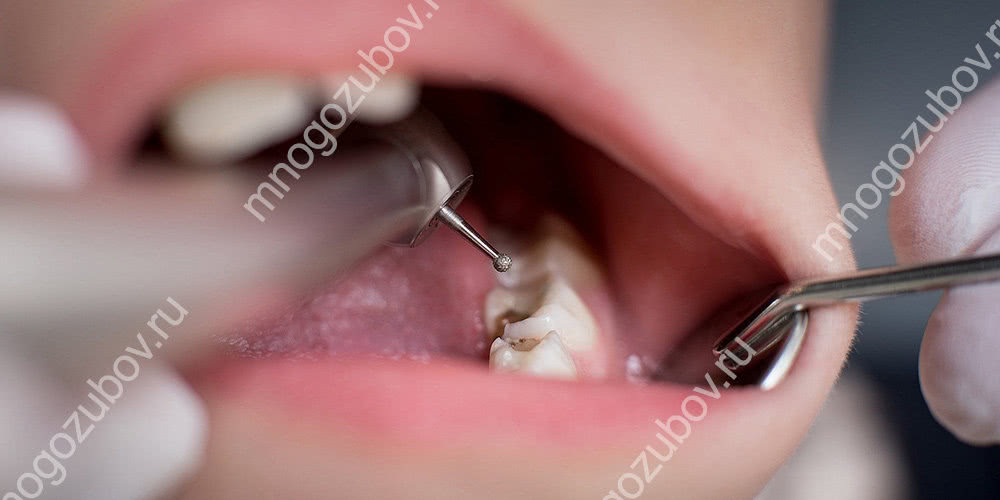
На заметку! Если патология началась извне, то одного лечения зуба недостаточно – нужно еще вылечить все ткани, которые его окружают (это называется «пародонт»). Лечение пародонтита проводится комплексно – т.е. консервативно и хирургически. Сначала при помощи кюретажа удаляется зубной камень и грануляционная ткань, а потом вносятся препараты для регенерации.

Хирургическое лечение

Если же перфорацию закрыть не удается, или отверстие размером 1-1,5 мм и более, то показано хирургическое вмешательство:

цистэктомия: так называется отсечение корня зуба,
гемисекция: в этом случае корень удаляется вместе с прилегающей частью коронки,
полное удаление с последующим протезированием.

«Мне во время лечения пульпита в поликлинике «пробили» бормашиной дыру до кости. Я, конечно, этого не почувствовал, но доктор даже в лице немного изменился. Думал, что удалять придется, но вроде бы пломба нормально встала. Хотя зубной сразу сказал, что это не надолго, а через года 3 придется удалять. Но я пока особых проблем не чувствую».

Андрей, 34 года, г. Киров, отзыв с сайта forum.stom.ru

Когда причиной патологии становится воспаление костной ткани или надкостницы, то часто требуется именно удаление (даже вместе с участком кости). Костный объем восполняется специальным трансплантатом, а через некоторое время устанавливается протез.

Приложения в полуклассической и квантовой физике

Теория бифуркации была применена, чтобы связать квантовые системы с динамикой их классических аналогов в атомных системах, молекулярные системы, и резонансные туннельные диоды. Теория бифуркации также применялась к изучению лазерная динамика и ряд теоретических примеров, к которым трудно получить экспериментальный доступ, таких как «взорванный верх» и связанные квантовые ямы. Основная причина связи между квантовыми системами и бифуркациями в классических уравнениях движения заключается в том, что при бифуркациях сигнатура классических орбит становится большой, поскольку Мартин Гуцвиллер указывает в своей классике работа над квантовый хаос. Многие виды бифуркаций были изучены в отношении связей между классической и квантовой динамикой, включая бифуркации седловых узлов, бифуркации Хопфа, омбилические бифуркации, бифуркации удвоения периода, бифуркации пересоединения, касательные бифуркации и бифуркации каспов.

Бифуркация в экономике

Определение в экономическом словаре гласит, что точка бифуркации в экономике — это момент ветвления и разделения вариантов развития экономики.

Приводят к этому внутренние флуктуации (изменения доходов, спроса и предложения, цен, урожайности, инновации, кредитование и многое другое) или внешние флуктуации (колебание курсов акций крупных корпораций, их крушение или возникновение, изменения таможенных норм, изменения климата и открытие месторождений полезных ископаемых и так далее).

Точки бифуркации дают широкий выбор путей развития экономики как в сторону аттрактора прогресса, так и в сторону аттрактора регресса. Экономисты–теоретики рассчитали законы периодичности вступления экономики в точки бифуркации, разрабатывают методы улучшения ситуации и прогнозирования аттракции систем.

Мотивы ввода / вывода

Несмотря на большую потенциальную сложность и разнообразие биологических сетей, все сетевое поведение первого порядка обобщается до одного из четырех возможных мотивов ввода-вывода: гиперболического или Михаэлиса-Ментен , сверхчувствительного , бистабильного и бистабильного необратимого (бистабильность, где отрицательная и, следовательно, для выхода из состояния высокой производительности необходим биологически невозможный ввод). Примеры каждого из них в биологическом контексте можно найти на соответствующих страницах.

Сверхчувствительные, бистабильные и необратимо бистабильные сети демонстрируют качественное изменение поведения сети вокруг определенных значений параметров — это их точки бифуркации.

От: admin

Эта тема закрыта для публикации ответов.