Оглавление
Распространенные заблуждения
Корреляция и причинно-следственная связь
Традиционное изречение, что « корреляция не подразумевает причинной связи », означает, что корреляция не может использоваться сама по себе для вывода причинной связи между переменными. Это изречение не должно означать, что корреляции не могут указывать на потенциальное существование причинно-следственных связей. Однако причины, лежащие в основе корреляции, если таковые имеются, могут быть косвенными и неизвестными, а высокие корреляции также пересекаются с отношениями идентичности ( тавтологиями ), где не существует причинных процессов. Следовательно, корреляция между двумя переменными не является достаточным условием для установления причинно-следственной связи (в любом направлении).
Эти примеры показывают, что коэффициент корреляции как сводная статистика не может заменить визуальный анализ данных. Иногда говорят, что примеры демонстрируют, что корреляция Пирсона предполагает, что данные следуют нормальному распределению , но это верно лишь отчасти. Корреляцию Пирсона можно точно рассчитать для любого распределения, имеющего конечную матрицу ковариаций , которая включает большинство распределений, встречающихся на практике. Однако коэффициент корреляции Пирсона (вместе с выборочным средним и дисперсией) является достаточной статистикой только в том случае, если данные взяты из многомерного нормального распределения. В результате коэффициент корреляции Пирсона полностью характеризует взаимосвязь между переменными тогда и только тогда, когда данные взяты из многомерного нормального распределения.
Коэффициент корреляции и ПАММ-счета
С расчётом корреляции я как студент экономического ВУЗа познакомился еще на втором курсе
Тем не менее, долгое время недооценивал важность расчёта корреляции именно для подбора ПАММ-портфеля. 2018 год очень четко показал, что ПАММ-счета с похожими стратегиями в случае кризиса могут вести себя очень похоже
Случилось так, что с середины года отказала не просто одна стратегия управляющего, а большинство торговых систем, завязанных на активные движения валютной пары EUR/USD:

Рынок был для каждого управляющего по-своему неблагоприятным, но присутствие их всех в портфеле привело к большой просадке. Совпадение? Не совсем, ведь это были ПАММ-счета с похожими элементами в торговых стратегиях. Без опыта торговли на рынке Форекс может быть сложно понять, как это работает, но по корреляционной таблице степень взаимосвязи видна и так:

Мы ранее рассматривали корреляцию вплоть до +1, но как видите на практике даже совпадение в районе 20-30% уже говорит о некоторой схожести ПАММ-счетов и, как следствие, результатов торговли.
Чтобы снизить шансы на повторение ситуации, как в 2018 году, я считаю в портфель стоит подбирать ПАММ-счета с низкой взаимной корреляцией. По сути, нам нужны уникальные стратегии с разными подходами и разными валютными парами для торговли. На практике, конечно, сложнее подобрать прибыльные счета с уникальными стратегиями, но если хорошо покопаться в рейтинге ПАММ-счетов, то все возможно. К тому же, низкая взаимная корреляция снижает требования для диверсификации, 5-6 счетов вполне хватит.
Пару слов о расчёте коэффициента корреляции для ПАММ-счетов. Достать сами данные относительно несложно, в Альпари прямо с сайта, для остальных площадок через сайт investflow.ru. Однако с ними нужно сделать небольшие преобразования.
Данные о прибыльности ПАММов изначально хранятся в формате накопленной доходности, нам это не подходит. Корреляция стандартных графиков доходности двух прибыльных ПАММ-счетов всегда будет очень высокой, просто потому что они все движутся в правый верхний угол:

У всех счетов положительная корреляция от 0.5 и выше за редким исключением, так мы ничего не поймем. Реальное сходство стратегий ПАММ-счетов можно увидеть только по дневным доходностям. Рассчитать их не особо сложно, если знаете нужные формулы доходности. Если прибыль или убыток двух ПАММ-счетов совпадают по дням и по процентам, высока вероятность что их стратегии имеют общие элементы — и коэффициент корреляции нам это покажет:

Как видите, некоторые корреляции стали нулевыми, а некоторые остались на высоком уровне. Мы теперь видим, какие ПАММ-счета действительно похожи между собой, а какие не имеют ничего общего.
Напоследок давайте разберёмся, что делать и как посчитать корреляцию, если у вас появилась в этом необходимость.
Вычисляем коэффициент корреляции.
Коэффициент корреляции — это показатель взаимного вероятностного влияния двух случайных величин.
Коэффициент корреляции R может принимать значения от -1 до +1. Если абсолютное значение находится ближе к 1,
то это свидетельство сильной связи между величинами, а если ближе к — то, это говорит о слабой связи или ее отсутствии. Если абсолютное значение
R равно единице, то можно говорить о функциональной связи между величинами, то есть одну величину можно
выразить через другую посредством математической функции.
| Rx,y | = |
|
( 1.1 ), где: |
cov( X,Y ) — ковариация случайных величин Х и Y
| σx2 | = |
|
|
(xk-Mx)2 , | σy2 | = |
|
|
(yk-My)2 ( 1.2 ), — оценки дисперсий случайных величин X и Y соответственно. |
| Mx | = |
|
|
xk , | My | = |
|
|
yk ( 1.3 ), — оценки математического ожидания случайных величин X и Y соответственно. |
| Rx,y | = |
|
( 1.4 ), где: |
| Mx | = |
|
|
xk , | My | = |
|
|
yk , | Mxy | = |
|
|
xkyk ( 1.5 ) |
| Sx2 | = |
|
|
xk2 — Mx2 , | Sy2 | = |
|
|
yk2 — My2 ( 1.6 ) |
На практике, для вычисления коэффициента корреляции чаще используется формула ( 1.4 )
т.к. она требует меньше вычислений. Однако если предварительно была вычислена ковариация cov(X,Y), то выгоднее использовать
формулу ( 1.1 ), т.к. кроме собственно значения ковариации можно воспользоваться и результатами промежуточных вычислений.
1.1 Вычислим коэффициент корреляции по формуле ( 1.4 ), для этого
вычислим значения xk2, yk2 и xkyk
и занесем их в таблицу 1.
Таблица 1
| k | xk | yk | хk2 | yk2 | хkyk |
| 1 | 2 | 3 | 4 | 5 | 6 |
| 1 | 25.2 | 30.8 | 635.04000 | 948.64000 | 776.16000 |
| 2 | 26.4 | 29.4 | 696.96000 | 864.36000 | 776.16000 |
| 3 | 26.0 | 30.2 | 676.00000 | 912.04000 | 785.20000 |
| 4 | 25.8 | 30.5 | 665.64000 | 930.25000 | 786.90000 |
| 5 | 24.9 | 31.4 | 620.01000 | 985.96000 | 781.86000 |
| 6 | 25.7 | 30.3 | 660.49000 | 918.09000 | 778.71000 |
| 7 | 25.7 | 30.4 | 660.49000 | 924.16000 | 781.28000 |
| 8 | 25.7 | 30.5 | 660.49000 | 930.25000 | 783.85000 |
| 9 | 26.1 | 29.9 | 681.21000 | 894.01000 | 780.39000 |
| 10 | 25.8 | 30.4 | 665.64000 | 924.16000 | 784.32000 |
| 11 | 25.9 | 30.3 | 670.81000 | 918.09000 | 784.77000 |
| 12 | 26.2 | 30.5 | 686.44000 | 930.25000 | 799.10000 |
| 13 | 25.6 | 30.6 | 655.36000 | 936.36000 | 783.36000 |
| 14 | 25.4 | 31 | 645.16000 | 961.00000 | 787.40000 |
| 15 | 26.6 | 29.6 | 707.56000 | 876.16000 | 787.36000 |
| 16 | 26.2 | 30.4 | 686.44000 | 924.16000 | 796.48000 |
| 17 | 26 | 30.7 | 676.00000 | 942.49000 | 798.20000 |
| 18 | 22.1 | 31.6 | 488.41000 | 998.56000 | 698.36000 |
| 19 | 25.9 | 30.5 | 670.81000 | 930.25000 | 789.95000 |
| 20 | 25.8 | 30.6 | 665.64000 | 936.36000 | 789.48000 |
| 21 | 25.9 | 30.7 | 670.81000 | 942.49000 | 795.13000 |
| 22 | 26.3 | 30.1 | 691.69000 | 906.01000 | 791.63000 |
| 23 | 26.1 | 30.6 | 681.21000 | 936.36000 | 798.66000 |
| 24 | 26 | 30.5 | 676.00000 | 930.25000 | 793.00000 |
| 25 | 26.4 | 30.7 | 696.96000 | 942.49000 | 810.48000 |
| 26 | 25.8 | 30.8 | 665.64000 | 948.64000 | 794.64000 |
1.2. Вычислим Mx по формуле ( 1.5 )1.2.1.xk12261.2.2.Mx = 25.7500001.3. Аналогичным образом вычислим My1.3.1.yk12261.3.2.My = 30.5000001.4. Аналогичным образом вычислим Mxy1.4.1.1.4.2.Mxy = 785.1088461.5. Вычислим значение Sx2 по формуле ( 1.6. )1.5.1.1.5.2.1.5.3.xx2Sx22 0.664811.6. Вычислим значение Sy2 по формуле ( 1.6. )1.6.1.1.6.2.1.6.3.yy2Sy22 0.205381.7. Вычислим произведение величин Sx2 и Sy2x2y21.8. Извлечем и последнего числа квадратный корень, получим значение SxSyxy1.9. Вычислим значение коэффициента корреляции по формуле (1.4.)ОТВЕТ: Rx,y = -0.720279
Матрицы корреляции
Корреляционная матрица случайных величин — это матрица, элементом которой является . Таким образом, диагональные элементы равны единице . Если меры корреляции используется коэффициенты продукта момент, корреляционная матрица является таким же , как ковариационная матрица из стандартизованных случайных величин для . Это применимо как к матрице корреляций совокупности (в этом случае — стандартное отклонение совокупности), так и к матрице корреляций выборки (в этом случае обозначает стандартное отклонение выборки). Следовательно, каждая из них обязательно является положительно-полуопределенной матрицей . Более того, корреляционная матрица является строго положительно определенной, если никакая переменная не может иметь все свои значения, точно сгенерированные как линейная функция значений других.
п{\ displaystyle n}Икс1,…,Иксп{\ Displaystyle X_ {1}, \ ldots, X_ {n}}п×п{\ Displaystyle п \ раз п}(я,j){\ displaystyle (я, j)}корр(Икся,Иксj){\ displaystyle \ operatorname {corr} (X_ {i}, X_ {j})} Иксяσ(Икся){\ Displaystyle X_ {i} / \ sigma (X_ {i})}язнак равно1,…,п{\ Displaystyle я = 1, \ точки, п}σ{\ displaystyle \ sigma}σ{\ displaystyle \ sigma}
Матрица корреляции является симметричной, потому что корреляция между и такая же, как корреляция между и .
Икся{\ displaystyle X_ {i}}Иксj{\ displaystyle X_ {j}}Иксj{\ displaystyle X_ {j}}Икся{\ displaystyle X_ {i}}
Матрица корреляции появляется, например, в одной формуле для , меры согласия в множественной регрессии .
В статистическом моделировании корреляционные матрицы, представляющие отношения между переменными, подразделяются на различные корреляционные структуры, которые различаются такими факторами, как количество параметров, необходимых для их оценки. Например, в заменяемой корреляционной матрице все пары переменных моделируются как имеющие одинаковую корреляцию, поэтому все недиагональные элементы матрицы равны друг другу. С другой стороны, авторегрессионная матрица часто используется, когда переменные представляют собой временной ряд, поскольку корреляции, вероятно, будут больше, когда измерения ближе по времени. Другие примеры включают независимый, неструктурированный, M-зависимый и Toeplitz.
В поисковом анализе данных , то иконография корреляций состоит в замене корреляционной матрицы на диаграмме , где «замечательные» корреляции представлены сплошной линией (положительная корреляция), или пунктирной линией (отрицательная корреляция).
Коэффициенты Пирсона и Спирмена
Рассмотрим два метода расчета.
Коэффициент Пирсона — это особый метод расчета взаимосвязи показателей между выраженностью численных значений в одной группе. Очень упрощенно он сводится к следующему:
- Берутся значения двух параметров в группе испытуемых (например, агрессии и перфекционизма).
- Находятся средние значения каждого параметра в группе.
- Находятся разности параметров каждого испытуемого и среднего значения.
- Эти разности подставляются в специальную форму для расчета коэффициента Пирсона.
Коэффициент ранговой корреляции Спирмена рассчитывается похожим образом:
- Берутся значения двух индикаторов в группе испытуемых.
- Находятся ранги каждого фактора в группе, то есть место в списке по возрастанию.
- Находятся разности рангов, возводятся в квадрат и суммируются.
- Далее разности рангов подставляются в специальную форму для вычисления коэффициента Спирмена.
В случае Пирсона расчет шел с использованием среднего значения. Следовательно, случайные выбросы данных (существенное отличие от среднего), например, из-за ошибки обработки или недостоверных ответов могут существенно исказить результат.
В случае Спирмена абсолютные значения данных не играют роли, так как учитывается только их взаимное расположение по отношению друг к другу (ранги). То есть, выбросы данных или другие неточности не окажут серьезного влияния на конечный результат.
Если результаты тестирования корректны, то различия коэффициентов Пирсона и Спирмена незначительны, при этом коэффициент Пирсона показывает более точное значение взаимосвязи данных.
Коэффициент корреляции Спирмена
В статистике также существует коэффициент корреляции Спирмена, который назван в честь статистика Чарльза Эдварда Спирмена (Spearman).
Цель этого коэффициента заключается в измерении интенсивности соотношения между двумя переменными, независимо от того, являются ли они линейными или нет.
Корреляция Спирмена служит для оценки того, может ли интенсивность взаимосвязи между двумя анализируемыми переменными быть измерена монотонной функцией (математическая функция, которая сохраняет или инвертирует соотношение начальной последовательности).
Как считать коэффициент корреляции Спирмена
Расчет коэффициента корреляции Спирмена уже немного отличается от предыдущей. Для этого необходимо организовать имеющиеся данные в следующую таблицу.
1. У вас должны быть две пары данных, соответствующих друг другу. Вы должны внести их в эту таблицу. Например, дирекция ресторана хочет узнать, есть ли связь между количеством заказов бутылок воды и количеством заказов десертов. Директор взял наугад данные 4-х столиков. Таким образом, у него получились две пары данных: где “Data А” — это заказы десертов, а “Data B” — заказы воды (т. е. первый столик заказал 7 десертов и 8 бутылок воды, второй — 6 десертов и 3 бутылки с водой и т. д.):
2. В столбце «Ranking А» мы будем классифицировать наблюдения, которые находятся в «Data А», нарастающим образом: «1» является самым низким значением в столбце и n (общее количество наблюдений) — самым высоким значением в столбце «Data А». В нашем примере это:
3. Сделайте то же самое позиционирование (классификацию наблюдений) для второго столбца “Data B”, записав это в столбце “Ranking B”.
4. В столбце «d» посчитайте разницу между двумя последними столбцами-ранкингами (A — B). Знак здесь учитывать не нужно (в следующем шаге узнаете почему).
5. Возведите во вторую степень каждое из значений, полученное в столбце «d».
6. Сделайте сумму всех данных, которые у вас получились в столбце «d2». Это будет Σd². В нашем примере Σd² = 0+1+0+1 = 2.
7. Теперь используем формулу Спирмена.
В нашем случае n = 4, мы это видим по количеству пар данных (соответствует числу наблюдений).
8. И наконец, замените данные в формуле.
Наш результат равен 0,8 или 80 %. Это означает, что переменные имеют положительную корреляцию.
Т. е. заказы бутылок воды и заказы десертов клиентами этого ресторана зависят друг от друга (т. к. коэффициент 0,8 далёк от 0), но не полностью (т. к. коэффициент очень близок к 1, но не равен 1). А положительная, так как коэффициент больше чем 0, это означает, что количество воды и количество десертов увеличиваются вместе, а не наоборот (т. е. чем выше количество потребляемой воды, тем выше количество потребляемых десертов).
Графическое представление коэффициента Фехнера
Пример №1. При разработке глинистого раствора с пониженной водоотдачей в высокотемпературных условиях проводили параллельное испытание двух рецептур, одна из которых содержала 2% КМЦ и 1% Na2CO3, а другая 2% КМЦ, 1% Na2CO3 и 0,1% бихромата калия. В результате получена следующие значения Х (водоотдача через 30 с).
| X1 | 9 | 9 | 11 | 9 | 8 | 11 | 10 | 8 | 10 |
| X2 | 10 | 11 | 10 | 12 | 11 | 12 | 12 | 10 | 9 |
Пример №2.
Коэффициент корреляции знаков, или коэффициент Фехнера, основан на оценке степени согласованности направлений отклонений индивидуальных значений факторного и результативного признаков от соответствующих средних. Вычисляется он следующим образом:
,
где na — число совпадений знаков отклонений индивидуальных величин от средней; nb — число несовпадений.
Коэффициент Фехнера может принимать значения от -1 до +1. Kф = 1 свидетельствует о возможном наличии прямой связи, Kф =-1 свидетельствует о возможном наличии обратной связи.
Рассмотрим на примере расчет коэффициента Фехнера по данным, приведенным в таблице:
|
Xi |
Yi |
Знаки отклонений значений признака от средней |
Совпадение (а) или несовпадение (в) знаков |
|
|
Для Xi |
Для Yi |
|||
|
8 |
40 |
— |
— |
А |
|
9 |
50 |
— |
+ |
В |
|
10 |
48 |
— |
+ |
В |
|
10 |
52 |
— |
+ |
В |
|
11 |
41 |
+ |
— |
В |
|
13 |
30 |
+ |
— |
В |
|
15 |
35 |
+ |
— |
В |
Для примера: .
Значение коэффициента свидетельствует о том, что можно предполагать наличие обратной связи.
Пример №2
Рассмотрим на примере расчет коэффициента Фехнера по данным, приведенным в таблице:
Средние значения:
|
Xi |
Yi |
Знаки отклонений от средней X |
Знаки отклонений от средней Y |
Совпадение (а) или несовпадение (b) знаков |
|
12 |
220 |
+ |
— |
B |
|
9 |
1070 |
— |
+ |
B |
|
8 |
1000 |
— |
+ |
B |
|
14 |
606 |
+ |
— |
B |
|
15 |
780 |
+ |
+ |
A |
|
10 |
790 |
— |
+ |
B |
|
10 |
900 |
— |
+ |
B |
|
15 |
544 |
+ |
— |
B |
|
93 |
5910 |
Значение коэффициента свидетельствует о том, что можно предполагать наличие обратной связи.
Интервальная оценка для коэффициента корреляции знаков
Пример №3.
Рассмотрим на примере расчет коэффициента корреляции знаков по данным, приведенным в таблице:
| Xi | Yi | Знаки отклонений от средней X | Знаки отклонений от средней Y | Совпадение (а) или несовпадение (b) знаков |
| 96 | 220 | + | — | B |
| 52 | 1070 | — | + | B |
| 60 | 1000 | — | + | B |
| 89 | 606 | + | — | B |
| 82 | 780 | + | + | A |
| 77 | 790 | — | + | B |
| 70 | 900 | — | + | B |
| 92 | 544 | + | — | B |
| 618 | 5910 |
Значение коэффициента свидетельствует о том, что можно предполагать наличие обратной связи.
Оценка коэффициента корреляции знаков. Значимость коэффициента корреляции знаков.
По таблице Стьюдента находим tтабл:
tтабл (n-m-1;a) = (6;0.05) = 1.943
Поскольку Tнабл > tтабл , то отклоняем гипотезу о равенстве 0 коэффициента корреляции знаков. Другими словами, коэффициент корреляции знаков статистически — значим.
Доверительный интервал для коэффициента корреляции знаков.
Доверительный интервал для коэффициента корреляции знаков.
r(-1;-0.4495)
Парная корреляция
Этот термин употребляется для обозначения взаимоотношений между двумя определенными величинами. Известно, что расходы на рекламу в США в значительной мере влияют на объем ВВП этой страны. Коэффициент корреляции между данными величинами по итогам наблюдений, продолжавшихся в течение 20 лет, составляет 0,9699.
Более «приземленный» пример – связь между посещаемостью страницы онлайн-магазина и объемом его продаж.
И уж, конечно, вряд ли кто-нибудь станет отрицать наличие зависимости, существующей между температурой воздуха и продажами пива или мороженого.
Корреляция – это взаимозависимость двух величин; коэффициент корреляции – это объективный показатель, определяющий степень этой взаимозависимости. Коэффициент корреляции может быть и положительным, и отрицательным. Что касается ценных бумаг, то они крайне редко бывают абсолютно коррелированными.
Наши группы:
Выборочный r и популяционный ρ
Аналогично среднему значению и стандартному отклонению, коэффициент корреляции является сводной статистикой. Он описывает выборку; в данном случае, выборку спаренных значений: роста и веса. Коэффициент корреляции известной выборки обозначается буквой r, тогда как коэффициент корреляции неизвестной популяции обозначается греческой буквой ρ (рхо).
Как мы убедились в предыдущей серии постов о тестировании гипотез, мы не должны исходить из того, что результаты, полученные в ходе измерения нашей выборки, применимы к популяции в целом. К примеру, наша популяция может состоять из всех пловцов всех недавних Олимпийских игр. И будет совершенно недопустимо обобщать, например, на другие олимпийские виды спорта, такие как тяжелая атлетика или фитнес-плавание.
Даже в допустимой популяции — такой как пловцы, выступавшие на недавних Олимпийских играх, — наша выборка коэффициента корреляции является всего лишь одной из многих потенциально возможных. То, насколько мы можем доверять нашему r, как оценке параметра ρ, зависит от двух факторов:
-
Размера выборки
-
Величины r
Безусловно, чем больше выборка, тем больше мы ей доверяем в том, что она представляет всю совокупность в целом. Возможно, не совсем интуитивно очевидно, но величина тоже оказывает влияние на степень нашей уверенности в том, что выборка представляет параметр . Это вызвано тем, что большие коэффициенты вряд ли возникли случайным образом или вследствие случайной ошибки при отборе.
Проверка статистических гипотез
В предыдущей серии постов мы познакомились с проверкой статистических гипотез, как средством количественной оценки вероятности, что конкретная гипотеза (как, например, что две выборки взяты из одной и той же популяции) истинная. Чтобы количественно оценить вероятность, что корреляция существует в более широкой популяции, мы воспользуемся той же самой процедурой.
В первую очередь, мы должны сформулировать две гипотезы, нулевую гипотезу и альтернативную:
H — это гипотеза, что корреляция в популяции нулевая. Другими словами, наше консервативное представление состоит в том, что измеренная корреляция целиком вызвана случайной ошибкой при отборе.
H1 — это альтернативная возможность, что корреляция в популяции не нулевая. Отметим, что мы не определяем направление корреляции, а только что она существует. Это означает, что мы выполняем двустороннюю проверку.
Стандартная ошибка коэффициента корреляции r по выборке задается следующей формулой:
Эта формула точна, только когда r находится близко к нулю (напомним, что величина ρ влияет на нашу уверенность), но к счастью, это именно то, что мы допускаем согласно нашей нулевой гипотезы.
Мы можем снова воспользоваться t-распределением и вычислить t-статистику:
В приведенной формуле df — это степень свободы наших данных. Для проверки корреляции степень свободы равна n — 2, где n — это размер выборки. Подставив это значение в формулу, получим:
В итоге получим t-значение 102.21. В целях его преобразования в p-значение мы должны обратиться к t-распределению. Библиотека scipy предоставляет интегральную функцию распределения (ИФР) для t-распределения в виде функции , и комплементарной ей (1-cdf) функции выживания . Значение функции выживания соответствует p-значению для односторонней проверки. Мы умножаем его на 2, потому что выполняем двустороннюю проверку:
P-значение настолько мало, что в сущности равно 0, означая, что шанс, что нулевая гипотеза является истинной, фактически не существует. Мы вынуждены принять альтернативную гипотезу о существовании корреляции.
Корреляционный анализ
Корреляционный анализ — метод обработки статистических данных, с помощью которого измеряется теснота связи между двумя или более переменными. Корреляционный анализ тесно связан с регрессионным анализом (также часто встречается термин «корреляционно-регрессионный анализ», который является более общим статистическим понятием), с его помощью определяют необходимость включения тех или иных факторов в уравнение множественной регрессии, а также оценивают полученное уравнение регрессии на соответствие выявленным связям (используя коэффициент детерминации).
Ограничения корреляционного анализа
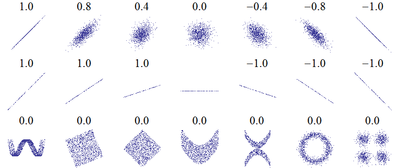
Множество корреляционных полей. Распределения значений (x,y){\displaystyle (x,y)} с соответствующими коэффициентами корреляций для каждого из них. Коэффициент корреляции отражает «зашумлённость» линейной зависимости (верхняя строка), но не описывает наклон линейной зависимости (средняя строка), и совсем не подходит для описания сложных, нелинейных зависимостей (нижняя строка). Для распределения, показанного в центре рисунка, коэффициент корреляции не определен, так как дисперсия y равна нулю.
- Применение возможно при наличии достаточного количества наблюдений для изучения. На практике считается, что число наблюдений должно не менее чем в 5-6 раз превышать число факторов (также встречается рекомендация использовать пропорцию, не менее чем в 10 раз превышающую количество факторов). В случае если число наблюдений превышает количество факторов в десятки раз, в действие вступает закон больших чисел, который обеспечивает взаимопогашение случайных колебаний.
- Необходимо, чтобы совокупность значений всех факторных и результативного признаков подчинялась многомерному нормальному распределению. В случае если объём совокупности недостаточен для проведения формального тестирования на нормальность распределения, то закон распределения определяется визуально на основе корреляционного поля. Если в расположении точек на этом поле наблюдается линейная тенденция, то можно предположить, что совокупность исходных данных подчиняется нормальному закону распределения.
- Исходная совокупность значений должна быть качественно однородной.
- Сам по себе факт корреляционной зависимости не даёт основания утверждать, что одна из переменных предшествует или является причиной изменений, или то, что переменные вообще причинно связаны между собой, а не наблюдается действие третьего фактора.
Область применения
Данный метод обработки статистических данных весьма популярен в экономике, астрофизике и социальных науках (в частности в психологии и социологии), хотя сфера применения коэффициентов корреляции обширна: контроль качества промышленной продукции, металловедение, агрохимия, гидробиология, биометрия и прочие. В различных прикладных отраслях приняты разные границы интервалов для оценки тесноты и значимости связи.
Популярность метода обусловлена двумя моментами: коэффициенты корреляции относительно просты в подсчете, их применение не требует специальной математической подготовки. В сочетании с простотой интерпретации, простота применения коэффициента привела к его широкому распространению в сфере анализа статистических данных.
Литература
- Wolfgang Härdle, Léopold Simar. Canonical Correlation Analysis // Applied Multivariate Statistical Analysis. — 2007. — ISBN 978-3-540-72243-4. — DOI:10.1007/978-3-540-72244-1_14.
- Knapp T. R. Canonical correlation analysis: A general parametric significance-testing system // Psychological Bulletin. — 1978. — Т. 85, вып. 2. — DOI:10.1037/0033-2909.85.2.410.
- Kanti V. Mardia, J. T. Kent, J. M. Bibby. Multivariate Analysis. — Academic Press, 1979.
- Hotelling H. Relations Between Two Sets of Variates // Biometrika. — 1936. — Т. 28, вып. 3–4. — DOI:10.1093/biomet/28.3-4.321.
- Hsu D., Kakade S. M., Zhang T. A spectral algorithm for learning Hidden Markov Models // Journal of Computer and System Sciences. — 2012. — Т. 78, вып. 5. — DOI:10.1016/j.jcss.2011.12.025. — arXiv:0811.4413.
- Huang S. Y., Lee M. H., Hsiao C. K. Nonlinear measures of association with kernel canonical correlation analysis and applications // Journal of Statistical Planning and Inference. — 2009. — Т. 139, вып. 7. — DOI:10.1016/j.jspi.2008.10.011.
- Sieranoja S., Sahidullah Md, Kinnunen T., Komulainen J., Hadid A. Audiovisual Synchrony Detection with Optimized Audio Features // IEEE 3rd Int. Conference on Signal and Image Processing (ICSIP 2018). — 2020. — Июль.
- Tofallis C. Model Building with Multiple Dependent Variables and Constraints // Journal of the Royal Statistical Society, Series D. — 1999. — Т. 48, вып. 3. — DOI:10.1111/1467-9884.00195. — arXiv:1109.0725.
- Degani A., Shafto M., Olson L. Canonical Correlation Analysis: Use of Composite Heliographs for Representing Multiple Patterns // Diagrammatic Representation and Inference. — 2006. — Т. 4045. — (Lecture Notes in Computer Science). — ISBN 978-3-540-35623-3. — DOI:10.1007/11783183_11.
- Jendoubi T., Strimmer K. A whitening approach to probabilistic canonical correlation analysis for omics data integration. — 2020.

Эта тема закрыта для публикации ответов.