Оглавление
ТРЕТИЙ СПОСОБ
Третий способ представления данных корреляционного анализа наиболее распространен как в Российских научных публикациях, так и в зарубежных. В заголовке таблицы указывается, что это корреляционная матрица, указывается также объем выборки (n).
Table 4. Matrix of Correlations between Intensity and Direction of the Components of Pre-Competitive Anxiety (Pineda-Espejel et al., 2013)
| 1 | 2 | 3 | 4 | 5 | ||
| 1 | Cognitive Anxiety Intensity | |||||
| 2 | Somatic Anxiety Intensity | .550** | ||||
| 3 | Self-Confidence Intensity | -.305* | -.126 | |||
| 4 | Cognitive Anxiety Direction | .035 | .076 | .013 | ||
| 5 | Somatic Anxiety Direction | .044 | .135 | -.125 | .537** | |
| 6 | Self-Confidence Direction | -.258 | -.167 | .564** | -.163 | -.161 |
** Correlation is significant to the level of .01.
* Correlation is significant to the level of .05.
Иногда корреляционная матрица выглядит следующим образом (табл. 5).
Таблица 5. Корреляционная матрица результатов различных вариантов жима штанги лежа (Penido L.N. et al., 2012)
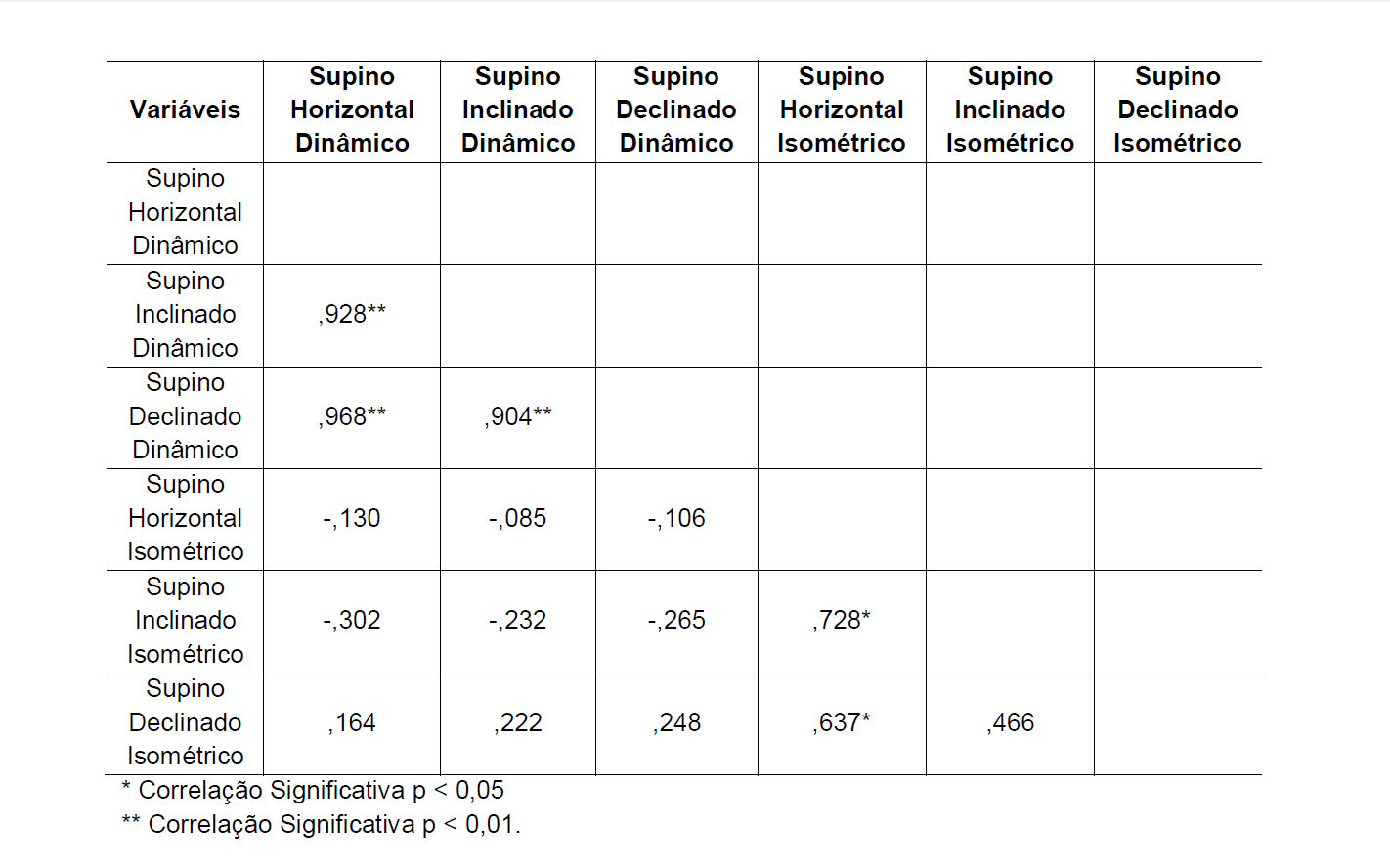
В этом случае авторы разместили коэффициенты корреляции слева-внизу, опустили нули в записи коэффициентов корреляции и не проставили цифру 1 на главной диагонали. Все это допускается при записи корреляционной матрицы.
Другие меры зависимости между случайными величинами
Информации, предоставляемой коэффициентом корреляции, недостаточно для определения структуры зависимости между случайными величинами. Коэффициент корреляции полностью определяет структуру зависимости только в очень частных случаях, например, когда распределение является многомерным нормальным распределением . (См. Диаграмму выше.) В случае эллиптических распределений он характеризует (гипер-) эллипсы одинаковой плотности; однако он не полностью характеризует структуру зависимости (например, степени свободы многомерного t-распределения определяют уровень хвостовой зависимости).
Корреляция расстояний была введена для устранения недостатка корреляции Пирсона, заключающейся в том, что она может быть равна нулю для зависимых случайных величин; корреляция нулевого расстояния подразумевает независимость.
Зависимость коэффициент Рандомизированной является вычислительно эффективной, копула основанной меры зависимости между многомерными случайными величинами. RDC инвариантен по отношению к нелинейным вычислениям случайных величин, способен обнаруживать широкий спектр функциональных паттернов ассоциации и принимает нулевое значение при независимости.
Для два двоичных переменных, то отношение шансов измеряет их зависимость, и занимает диапазон неотрицательных чисел, возможно , бесконечность: . Похожие статистические данные , такие как Юла в Y и Юле в Q нормализуют это корреляции-как диапазон . Отношение шансов обобщается логистической моделью для моделирования случаев, когда зависимые переменные являются дискретными и могут быть одна или несколько независимых переменных.
,+∞{\ displaystyle }-1,1{\ displaystyle }
Коэффициент корреляции , основанная на энтропии взаимная информация , общая корреляция , двойная полная корреляция и полихорическая корреляция также способны обнаруживать более общие зависимости, как и рассмотрение связки между ними, в то время как коэффициент детерминации обобщает коэффициент корреляции на множественную регрессию. .
ЦТР как фактор риска развития глаукомы
Согласно исследованию Ocular Hypertension Treatment Study (OHTS, исследование лечения глазной гипертензии) тонкая роговица рассматривается как фактор риска развития глаукомы . Однако более поздние исследования поставили под сомнение значение тонкой роговицы как фактора риска . В метааналитическом исследовании R. Gaspar et al. (2017) также указывают на неоднозначные результаты исследований последних лет относительно истинного значения ЦТР как фактора риска развития глаукомы. Так, некоторые исследования подтверждают, что тонкая ЦТР является фактором риска развития глаукомы , а в других не обнаружено статистически значимой корреляционной разницы между значениями ВГД и ЦТР . Вместе с тем, согласно данным R. Gaspar et al. (2017), значения ЦТР значительно ниже у пациентов с глаукомой по сравнению с таковыми в контрольной группе. Авторы подчеркивают влияние ЦТР на результаты тонометрии, не относя данный параметр к числу самостоятельных факторов риска заболевания . ЦТР может служить индикатором анатомических особенностей и свидетельствовать об эластичности и растяжимости тканей глазного яблока . В ряде исследований была выявлена корреляция ЦТР с глаукомными структурными изменениями диска зрительного нерва (ДЗН) .
Что такое ложная корреляция
В статистике ложная корреляция или ложная связь относится к связи между двумя переменными, которая кажется причинной, но не является таковой. Ложные отношения часто выглядят как одна переменная, влияющая на другую. Эта ложная корреляция часто вызвана третьим фактором, который не очевиден во время исследования, который иногда называют смешивающим фактором.
Ключевые выводы
- Ложная корреляция, или ложная корреляция, – это когда два фактора кажутся случайно связанными, но не связаны.
- Появление причинно-следственной связи часто происходит из-за аналогичного движения на карте, которое оказывается случайным или вызванным третьим «смешивающим» фактором.
- Ложная корреляция часто может быть вызвана малым размером выборки или произвольными конечными точками.
BREAKING DOWN «Отрицательная корреляция»
Отрицательная корреляция используется в статистике для измерения суммы, которую изменение одной переменной может повлиять на противоположное изменение в другой переменной. Для количественной оценки предсказуемости отрицательной взаимосвязи между двумя переменными аналитики проводят регрессионный анализ. Эта процедура предоставляет аналитикам расчет R-квадрата (R2), который является статистическим показателем того, насколько хорошо одна переменная предсказывает значение другой переменной. Если R2 между двумя отдельными элементами равно 1, это означает, что независимая переменная точно прогнозирует зависимую переменную без ошибок. R2 из 0 означает, что независимая переменная не может предсказать зависимую переменную. R2, который находится между 0 и 1, измеряет степень, в которой независимая переменная предсказывает зависимую переменную. Например, если R2 равно 0. 4, это означает, что независимая переменная может предсказать зависимую переменную с точностью 40%.
Например, чем больше времени человек проводит в торговом центре, покупая товары, тем меньше денег у него на его текущем счете. Чем выше коэффициент взаимных инвестиций инвестора, тем ниже его доходность инвестиций. Чем больше часов человек проводит в офисе, тем меньше времени у него на другие занятия. Все эти переменные имеют отрицательный R2.
Распространенные заблуждения
Корреляция и причинно-следственная связь
Традиционное изречение, что « корреляция не подразумевает причинной связи », означает, что корреляция не может использоваться сама по себе для вывода причинной связи между переменными. Это изречение не должно означать, что корреляции не могут указывать на потенциальное существование причинно-следственных связей. Однако причины, лежащие в основе корреляции, если таковые имеются, могут быть косвенными и неизвестными, а высокие корреляции также пересекаются с отношениями идентичности ( тавтологиями ), где не существует причинных процессов. Следовательно, корреляция между двумя переменными не является достаточным условием для установления причинно-следственной связи (в любом направлении).
Корреляция между возрастом и ростом у детей довольно прозрачна с точки зрения причинно-следственной связи, но корреляция между настроением и здоровьем людей менее очевидна. Приводит ли улучшение настроения к улучшению здоровья, или хорошее здоровье приводит к хорошему настроению, или и то, и другое? Или в основе обоих лежит какой-то другой фактор? Другими словами, корреляция может рассматриваться как свидетельство возможной причинной связи, но не может указывать на то, какой может быть причинная связь, если таковая имеется.
Простые линейные корреляции
Четыре набора данных с одинаковой корреляцией 0,816
Коэффициент корреляции Пирсона указывает на силу линейной связи между двумя переменными, но его значение, как правило, не полностью характеризует их взаимосвязь. В частности, если условное среднее из дано , обозначается , не является линейным в , коэффициент корреляции будет не в полной мере определить форму .
Y{\ displaystyle Y}Икс{\ displaystyle X}E(Y∣Икс){\ displaystyle \ operatorname {E} (Y \ mid X)}Икс{\ displaystyle X}E(Y∣Икс){\ displaystyle \ operatorname {E} (Y \ mid X)}
Прилегающие изображение показывает разброс участков из квартет энскомбы , набор из четырех различных пар переменных , созданный Фрэнсис Анскомбами . Четыре переменные имеют одинаковое среднее значение (7,5), дисперсию (4,12), корреляцию (0,816) и линию регрессии ( y = 3 + 0,5 x ). Однако, как видно на графиках, распределение переменных сильно отличается. Первый (вверху слева), кажется, распределен нормально и соответствует тому, что можно было бы ожидать, рассматривая две коррелированные переменные и следуя предположению о нормальности. Второй (вверху справа) не распространяется нормально; хотя можно наблюдать очевидную взаимосвязь между двумя переменными, она не является линейной. В этом случае коэффициент корреляции Пирсона не указывает на то, что существует точная функциональная связь: только степень, в которой эта связь может быть аппроксимирована линейной зависимостью. В третьем случае (внизу слева) линейная зависимость идеальна, за исключением одного выброса, который оказывает достаточное влияние, чтобы снизить коэффициент корреляции с 1 до 0,816. Наконец, четвертый пример (внизу справа) показывает другой пример, когда одного выброса достаточно для получения высокого коэффициента корреляции, даже если связь между двумя переменными не является линейной.
у{\ displaystyle y}
Эти примеры показывают, что коэффициент корреляции как сводная статистика не может заменить визуальный анализ данных. Иногда говорят, что примеры демонстрируют, что корреляция Пирсона предполагает, что данные следуют нормальному распределению , но это верно лишь отчасти. Корреляцию Пирсона можно точно рассчитать для любого распределения, имеющего конечную матрицу ковариаций , которая включает большинство распределений, встречающихся на практике. Однако коэффициент корреляции Пирсона (вместе с выборочным средним и дисперсией) является достаточной статистикой только в том случае, если данные взяты из многомерного нормального распределения. В результате коэффициент корреляции Пирсона полностью характеризует взаимосвязь между переменными тогда и только тогда, когда данные взяты из многомерного нормального распределения.
Корреляция Пирсона
Коэффициент корреляции Пирсона (названный по имени Карла Пирсона) можно использовать для обобщения силы линейной зависимости между двумя выборками данных.
Коэффициент корреляции Пирсона рассчитывается как ковариация двух переменных, деленная на произведение стандартного отклонения каждой выборки данных. Это нормализация ковариации между двумя переменными для получения интерпретируемой оценки.
Использование среднего значения и стандартного отклонения в расчете предполагает необходимость того, чтобы две выборки данных имели гауссово или гауссовидное распределение.
В результате расчета коэффициент корреляции можно интерпретировать, чтобы понять взаимосвязь.
Коэффициент возвращает значение от -1 до 1, которое представляет пределы корреляции от полной отрицательной корреляции до полной положительной корреляции. Значение 0 означает отсутствие корреляции. Значение следует интерпретировать, где часто значение ниже -0,5 или выше 0,5 указывает на заметную корреляцию, а значения ниже этих значений указывают на менее заметную корреляцию.
pearsonr ()Функция SciPy может использоваться для расчета коэффициента корреляции Пирсона между двумя выборками данных одинаковой длины.
Мы можем вычислить корреляцию между двумя переменными в нашей тестовой задаче.
Полный пример приведен ниже.
При выполнении примера вычисляется и печатается коэффициент корреляции Пирсона.
Мы можем видеть, что две переменные положительно коррелируют и что корреляция составляет 0,8. Это говорит о высоком уровне корреляции, например значение выше 0,5 и близко к 1,0.
Коэффициент корреляции Пирсона можно использовать для оценки взаимосвязи между более чем двумя переменными.
Это можно сделать, рассчитав матрицу отношений между каждой парой переменных в наборе данных. Результатом является симметричная матрица, называемая корреляционной матрицей со значением 1,0 вдоль главной диагонали, поскольку каждый столбец всегда идеально коррелирует с самим собой.
Слово предостережения
Наконец, слово предостережения. Корреляция между двумя переменнымиИкса такжеYявляется ли оно линейным или нелинейным, не означает автоматически причинно-следственную связь междуИкса такжеY(пока верно обратное). Даже когда наблюдается большая корреляция междуИкса такжеY,Иксне может напрямую влиятьYили наоборот. Может быть, есть скрытая переменная, называемая смешанной переменной, которая одновременно влияет на обаИкса такжеYтак что они поднимаются и падают синхронно друг с другом. Для иллюстрации рассмотрим следующий график, который показывает два набора данных, нанесенных друг на друга
ВотИксЭто временной ряд, который варьируется от 1990 до 2016 года и содержит долю населения мира, имеющего доступ к электричеству в каждый из этих лет. ПеременнаяYЭто также временной ряд, который варьируется от 1990 до 2016 года и содержит численность рабочей силы во всем мире в каждый из этих лет.
Два набора данных явно сильно коррелированы. Вы будете судить, есть ли причина и следствие!
Ковариантность прекрасна, но …
Ковариантность — это прекрасный способ количественно оценить движение переменных относительно друг друга, но у него есть некоторые проблемы.
Отличающиеся единицы:Ковариацию трудно интерпретировать, когда единицы двух переменных различны. Например, еслиИксв долларах иYнаходится в фунтах стерлингов единица ковариации междуИкса такжеYстановитсядолларовые времена фунт стерлингов, Как можно это интерпретировать? Даже когда обаИкса такжеYимеют одну и ту же единицу, скажем, доллар, единицы ковариации становится …доллар раз доллар!Все еще не легко понять. Облом!
Отличающиеся весы:Существует также проблема дальности. когдаИкса такжеYварьируются в течение небольшого интервала, скажемвы получите обманчиво крошечное значение ковариации, даже еслиИкса такжеYдвигаться вместе очень плотно.
Сложность со сравнением:Потому чтоИкса такжеYмогут иметь разные единицы измерения и разные диапазоны, зачастую невозможно объективно сравнить ковариацию между одной парой переменных и другой парой переменных. Скажи я хочу сравнитьнасколько сильнее или слабееэто линейная зависимость междуэкономия топлива и длина автомобиляпо сравнению с отношением междуэкономия топлива и снаряженная масса, Использование ковариации для этого сравнения потребует сравнения двух значений в двух разных единицах и двух разных диапазонах. Проблематично, если не сказать больше.
Если бы мы только могли масштабировать ковариацию, чтобы диапазон был стандартизирован, а также решить проблему «единиц» Введите «стандартное отклонение». Проще говоря, стандартное отклонение измеряет среднее отклонение данных от их среднего значения. Стандартное отклонение также имеет приятное свойство: он имеет ту же единицу, что и исходная переменная. Итак, давайте разделим ковариацию на стандартные отклонения двух переменных. Это приведет к изменению масштаба ковариации, так что теперь она выражается вкратные стандартному отклонениюи это будет такжеотмените единицы измерения из числителя, Все неприятности с ковариацией решаются в двух простых делениях! Вот полученная формула:
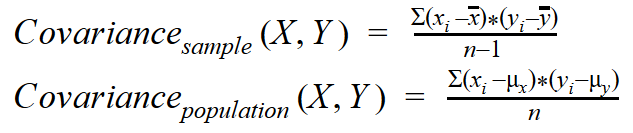
Где же мы видели эту формулу раньше? Это, конечно, коэффициент корреляции Пирсона!
Положительная корреляция против обратной корреляции: обзор
В области статистики корреляция описывает взаимосвязь между двумя переменными. Переменные коррелируют, если за изменением одной следует изменение другой. Корреляция показывает, являются ли отношения положительными или отрицательными и насколько они сильны. Положительная корреляция описывает взаимосвязь между двумя переменными, которые изменяются вместе, а обратная корреляция описывает взаимосвязь между двумя переменными, которые изменяются в противоположных направлениях. Обратную корреляцию иногда называют отрицательной корреляцией, которая описывает один и тот же тип взаимосвязи между переменными.
Ключевые выводы
- Положительная корреляция существует, когда две связанные переменные движутся в одном направлении.
- Обратная корреляция существует, когда две связанные переменные движутся в противоположном направлении.
- Корреляция не обязательно подразумевает причинно-следственную связь, поскольку на направление могут влиять другие факторы.
Формула для коэффициента Пирсона
Формула для коэффициента корреляции между двумя переменными, которые имеютлинейное отношениеявляется:

Формула для коэффициента корреляции между переменными X и Y
Две сигмы в знаменателе являются стандартными отклонениями соответствующих переменных. Мы будем анализироватьковариациив немного.
Между тем отметим, что при расчете по приведенной выше формуле коэффициент корреляции называетсяКоэффициент корреляции Пирсона.Он представлен символом ‘р’При использовании для образца и по символурокогда используется для всей совокупности ценностей.
Если вы хотите использовать «популяционную версию» этой формулы, обязательно используйте «популяционные формулы» для ковариации и стандартного отклонения.
Пример: акции против облигаций
Исторически акции и облигации как широкие классы активов демонстрировали длительные периоды отрицательной корреляции (хотя это не всегда так). Вот почему большинство финансовых профессионалов рекомендуют портфель, состоящий как из акций, так и из облигаций.
Причина, по которой облигации имеют тенденцию расти, когда акции падают, и наоборот, может быть объяснена рядом гипотез. Первый предполагает стремление к качеству. Когда акции становятся волатильными или переживают «медвежий» рынок, инвесторы могут попытаться вложить свои деньги в более консервативные инвестиции, такие как облигации. В то же время рынки, как правило, падают в периоды экономического спада, а процентные ставки также падают во время рецессии. Когда процентные ставки падают (вместе с ценами на акции), цены облигаций реагируют обратно и вырастают.
#О
Использование корреляции как научного доказательства
Многие научные данные основаны на корреляции переменных — они наблюдаются вместе
Ученые осторожно указывают на то, что корреляция не обязательно означает причинную связь. Предположение, что A вызывает B просто потому, что A коррелирует с B, часто не принимается в качестве законной формы аргумента.
Однако иногда люди допускают противоположное заблуждение — полностью игнорируют корреляцию. Это отвергнет большое количество важных научных данных. Поскольку проведение контролируемых двойных слепых исследований может быть трудным или этически невозможным , корреляционные доказательства с нескольких разных точек зрения могут быть полезны для прогнозирования, несмотря на то, что они не могут предоставить доказательства причинно-следственной связи . Например, социальные работники могут быть заинтересованы в том, чтобы узнать, как жестокое обращение с детьми связано с успеваемостью. Хотя было бы неэтично проводить эксперимент, в котором детей случайным образом распределяют, чтобы они получали или не подвергались насилию, исследователи могут изучить существующие группы, используя неэкспериментальный корреляционный план. Если на самом деле существует отрицательная корреляция между жестоким обращением и успеваемостью, исследователи потенциально могут использовать это знание статистической корреляции, чтобы делать прогнозы о детях вне исследования, которые подвергаются жестокому обращению, даже если исследование не предоставило причинно-следственных доказательств того, что насилие снижает академическую успеваемость. Комбинация ограниченных доступных методологий с отклонением ошибки корреляции иногда использовалась для противодействия научным открытиям. Например, табачная промышленность исторически полагалась на отклонение корреляционных данных, чтобы отвергнуть связь между табаком и раком легких , как это делал биолог и статистик Рональд Фишер , часто в ее пользу.
Корреляция — это ценный вид научных данных в таких областях, как медицина, психология и социология. Корреляции сначала должны быть подтверждены как реальные, а затем необходимо систематически исследовать все возможные причинные отношения. В конце концов, корреляция сама по себе не может использоваться в качестве доказательства причинно-следственной связи между лечением и пользой, фактором риска и заболеванием, или социальным или экономическим фактором и различными результатами. Это один из наиболее часто используемых типов доказательств, потому что легко и даже соблазнительно прийти к преждевременным выводам, основанным на предварительном появлении корреляции.
Что такое корреляция?
Переменные в наборе данных могут быть связаны по многим причинам.
Например:
- Одна переменная может вызывать или зависеть от значений другой переменной.
- Одна переменная может быть легко связана с другой переменной.
- Две переменные могут зависеть от третьей неизвестной переменной.
Это может быть полезно при анализе данных и моделировании, чтобы лучше понять взаимосвязи между переменными. Статистическая связь между двумя переменными называется их корреляцией.
Корреляция может быть положительной, что означает, что обе переменные движутся в одном и том же направлении, или отрицательной, что означает, что когда значение одной переменной увеличивается, значения других переменных уменьшаются. Корреляция также может быть нейронной или нулевой, что означает, что переменные не связаны.
- Положительное соотношение: обе переменные изменяются в одном направлении.
- Нейтральная корреляция: Нет связи в изменении переменных.
- Отрицательная корреляция: переменные меняются в противоположных направлениях.
Производительность некоторых алгоритмов может ухудшиться, если две или более переменных тесно связаны между собой, что называется мультиколлинеарностью. Примером является линейная регрессия, где одна из нарушенных коррелированных переменных должна быть удалена, чтобы улучшить навыки модели.
Мы также можем быть заинтересованы в корреляции между входными переменными и выходной переменной, чтобы дать представление о том, какие переменные могут или не могут иметь значение в качестве входных данных для разработки модели.
Структура отношений может быть известна, например, оно может быть линейным, или мы можем не иметь представления, существует ли связь между двумя переменными или какую структуру она может принять. В зависимости от того, что известно о взаимосвязи и распределении переменных, могут быть рассчитаны различные оценки корреляции.
В этом уроке мы рассмотрим одну оценку для переменных, которые имеют гауссово распределение и линейную зависимость, а другую — не предполагающую распределение и сообщим о любых монотонных (увеличивающихся или уменьшающихся) отношениях.
Как рассчитать коэффициент корреляции в Excel
В сегодняшней статье речь пойдет о том, как переменные могут быть связаны друг с другом. С помощью корреляции мы сможем определить, существует ли связь между первой и второй переменной. Надеюсь, это занятие покажется вам не менее увлекательным, чем предыдущие!
Корреляция измеряет мощность и направление связи между x и y. На рисунке представлены различные типы корреляции в виде графиков рассеяния упорядоченных пар (x, y). По традиции переменная х размещается на горизонтальной оси, а y — на вертикальной.
График А являет собой пример положительной линейной корреляции: при увеличении х также увеличивается у, причем линейно. График В показывает нам пример отрицательной линейной корреляции, на котором при увеличении х у линейно уменьшается. На графике С мы видим отсутствие корреляции между х и у. Эти переменные никоим образом не влияют друг на друга.
Наконец, график D — это пример нелинейных отношений между переменными. По мере увеличения х у сначала уменьшается, потом меняет направление и увеличивается.
Оставшаяся часть статьи посвящена линейным взаимосвязям между зависимой и независимой переменными.
Коэффициент корреляции
Коэффициент корреляции, r, предоставляет нам как силу, так и направление связи между независимой и зависимой переменными. Значения r находятся в диапазоне между — 1.0 и + 1.0. Когда r имеет положительное значение, связь между х и у является положительной (график A на рисунке), а когда значение r отрицательно, связь также отрицательна (график В). Коэффициент корреляции, близкий к нулевому значению, свидетельствует о том, что между х и у связи не существует график С).
Сила связи между х и у определяется близостью коэффициента корреляции к — 1.0 или +- 1.0. Изучите следующий рисунок.
График A показывает идеальную положительную корреляцию между х и у при r = + 1.0. График В — идеальная отрицательная корреляция между х и у при r = — 1.0. Графики С и D — примеры более слабых связей между зависимой и независимой переменными.
Коэффициент корреляции, r, определяет, как силу, так и направление связи между зависимой и независимой переменными. Значения r находятся в диапазоне от — 1.0 (сильная отрицательная связь) до + 1.0 (сильная положительная связь). При r= 0 между переменными х и у нет никакой связи.
Мы можем вычислить фактический коэффициент корреляции с помощью следующего уравнения:
Ну и ну! Я знаю, что выглядит это уравнение как страшное нагромождение непонятных символов, но прежде чем ударяться в панику, давайте применим к нему пример с экзаменационной оценкой. Допустим, я хочу определить, существует ли связь между количеством часов, посвященных студентом изучению статистики, и финальной экзаменационной оценкой. Таблица, представленная ниже, поможет нам разбить это уравнение на несколько несложных вычислений и сделать их более управляемыми.
Как видите, между числом часов, посвященных изучению предмета, и экзаменационной оценкой существует весьма сильная положительная корреляция. Преподаватели будут весьма рады узнать об этом.
Какова выгода устанавливать связь между подобными переменными? Отличный вопрос. Если обнаруживается, что связь существует, мы можем предугадать экзаменационные результаты на основе определенного количества часов, посвященных изучению предмета. Проще говоря, чем сильнее связь, тем точнее будет наше предсказание.
Использование Excel для вычисления коэффициентов корреляции
Я уверен, что, взглянув на эти ужасные вычисления коэффициентов корреляции, вы испытаете истинную радость, узнав, что программа Excel может выполнить за вас всю эту работу с помощью функции КОРРЕЛ со следующими характеристиками:
КОРРЕЛ (массив 1; массив 2),
массив 1 = диапазон данных для первой переменной,
массив 2 = диапазон данных для второй переменной.
Например, на рисунке показана функция КОРРЕЛ, используемая при вычислении коэффициента корреляции для примера с экзаменационной оценкой.
Корреляционная функция
Для графического отображения полученных результатов применяют корреляционную функцию (КФ), являющуюся зависимостью коэффициента корреляции явления от временного сдвига (лага). Существует два вида КФ: классическая, или техническая, и интервальная (рис. 7 и рис. 8 соответственно). Классическая корреляционная функция для анализа ЭЭГ не подходит, т.к. при разных t анализу будут подлежать участки разной протяженности, а для сопоставимости коэффициентов корреляции это допустимо только в случае стационарности процессов, которые сохраняют свои свойства на всей протяженности.
Классическая корреляционная функция имеет недостатки:
- невозможность сопоставлять коэффициенты корреляции, которые были вычислены для фрагментов ЭЭГ с различной протяженностью, поскольку полученные коэффициенты будут иметь разные характеристики (т.к. ЭЭГ не является стационарным процессом)
- размер выборки может отличаться; величины на одном конце функции могут быть значимые, а на другом – нет.
Рисунок 7. Классическая, или техническая, корреляционная функция
При построении интервальной корреляционной функции на записи сигнала обращают внимание на корреляционный образец χ длиной Δt, от которого начинается эпоха анализа Т. Чтобы найти связь между явлениями χ при изменении t, необходим анализ равноразмерных участков γ, которые сдвинуты относительно χ на значение τ
(рис. 8)
Если сравнивать интервальную и классическую корреляционные функции, то можно заметить, что интервальная функция имеет несколько преимуществ:
- Используется чаще при выявлении задержек в ЭЭГ-сигнале;
- Повторение этапов высоких значений при сдвигах образца;
- Ее легко интерпретировать.
При исследовании интервальной корреляционной функции необходимо отметить, что высокие значения функции при автокорреляции – это возможное следствие возврата к исходному функциональному состоянию, а в случае кросскорреляционной функции – задержки передачи сигнала между отведениями.
Рисунок 8. Интервальная корреляционная функция
Наиболее чувствительный метод для поиска различий в ЭЭГ-сигналах – огибающая ЭЭГ, оценивающая меру синхронности или асинхронности изменений постсинаптических потенциалов в исследуемых отведениях (амплитуда сигнала повышается при одновременном изменении двух сигналов).

Эта тема закрыта для публикации ответов.